Home | Download | Documents | Tips & Tutorials | Code Library | Help / User Group | Order

Loops and Fractals

This lesson shows you how to control the order in which your filter processes image pixels by using FM's ForEveryPixel and ForEveryTile handlers in conjunction with for-loops.

This lesson also introduces floating-point arithmetic and the FM built-in functions abs(), src(), pset(), setCtlRange(), updateProgress(), and testAbort().

Throughout this lesson we assume that the host graphics application is Adobe Photoshop 4.0.  The instructions for other hosts may vary.
 

Photoshop 4.0-specific information is flagged with this icon.

Information for Paint Shop Pro is flagged with this icon.

Features that are not yet implemented are flagged with this icon.

Useful tips, techniques, and hints are marked with this icon.

This icon indicates a feature that may cause harmful results if improperly used.

 

1. Rolling Your Own Loops

The Filter Designer's sole task is to create a formula for each pixel channel (or plane) that defines the value assigned to each pixel channel as it is processed.

Many image processing algorithms fit naturally into this paradigm, and even more algorithms can be forced to fit (albeit less naturally).

However, there are large classes of algorithms which are difficult to express in this paradigm.  FM gives the Filter Designer much greater freedom by allowing the FD to take control of the image processing at the tile, row, or pixel level.  At each level, the FD can explicitly control the order of processing by coding his own loops using the various control constructs of the FF+ language.

In this lesson we will concentrate on controlling the image processing at the tile or pixel level using for-loops.

2. ForEveryPixel

   

3. ForEveryTile

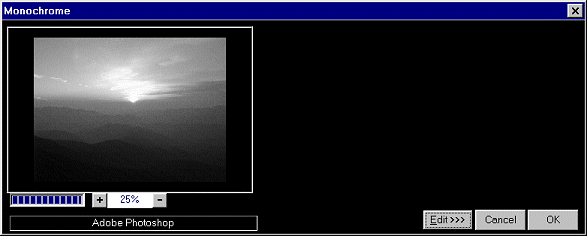
At the highest level, FilterMeister processes an image one "tile" at a time, where a tile is a large rectangular section of the input image. The size of each tile is chosen to minimize physical RAM requirements while processing an image.  The tile size also depends on the properties of the image processing algorithm.  Some algorithms are inherently not tileable; for such "untileable" algorithms, the tile size is set equal to the size of the entire input image, and only one such tile is processed per filter application.

By default, FM takes a conservative approach and considers an algorithm to be untileable.  So in the remainder of this lesson, we will assume that each image is processed as a single large tile.  The subtleties of writing "tileable" algorithms will be discussed in a future lesson.

The ForEveryTile handler is invoked once for each tile in the input image (which in the following examples means it is invoked once per filter application, with a single tile containing the entire input image).

Within the ForEveryTile handler, the Filter Designer is free to process the pixels in any desired order (or even not to process some of them). The FF+ for-loop construct is useful for controlling the order in which pixels are processed.

4. For-loops

    for ( <initialization> ; <while-condition> ; <iteration-update> )
    {
        <body-statements>;
    }

where:

• the <initialization> expression is executed once at the beginning of the loop to perform any required loop initialization, such as setting the initial value of a counter;

 
• the <while-condition> expression is evaluated before each iteration of the loop; if true, the body of the loop is executed; otherwise, the loop terminates and execution proceeds with the statements following the end of the for-loop;

 
• the <iteration-update> expression is executed after every execution of the loop body, and typically is used to update the value of a counter or pointer before the next pass through the loop;

 
• the <body-statements> form the "body" of the loop, and are executed once per iteration through the for-loop.  (Note that the <body-statements> are not executed at all if the initial evaluation of the <while-condition> is false.)

In the following program, we use nested for-loops to iterate through all the pixels of an image, and all channels within each pixel.  The outer for-loop iterates the x-coordinate (i.e., it iterates left-to-right or column-by-column), the first inner loop iterates the y-coordinate (from top-to-bottom or row-by-row), and the innermost loop iterates through the individual channels of each pixel (the "z" coordinate). Since an inner loop executes many times per iteration of an outer loop, this means that the y-coordinate varies faster than the x-coordinate. Thus, we are processing the image column-by-column rather than row-by-row. This is the transpose of the order in which Filter Factory normally processes an image.
 

%ffp   Title:"Brightness"   ctl(5):"Brightness %",val=50,range=(0,100)   ForEveryTile:   {       for (x=0; x < X; x++) {           for (y=0; y < Y; y++) {               for (z=0; z < Z; z++) {                   pset(x,y,z,src(x,y,z)*ctl(5)/100);               }           }       }       true;  //Done!   }

 

TIP

Processing an image in column-by-column order rather than row-by-row order may be useful and important for some algorithms. However, since the image is laid out row-by-row in memory, it is generally more efficient to process row-by-row.  Specifically, processing column-by-column may greatly increase the number of page faults for very large images, resulting in slow performance. So if everything else is equal, choose row-by-row rather than column-by-column processing order.

 
The body of the innermost for-loop in the example above is a single statement:

        pset(x, y, z, src(x,y,z)*ctl(5)/100);
 
The FF/FF+ built-in function src(x,y,z) returns the value of channel z for the input pixel at coordinates (x,y).

The FF+ built-in function pset(x,y,z,v) sets channel z of the output pixel at coordinates (x,y) to the value v.  The value of v is clamped to the range [0,255] before making the assignment.

So the effect of the loop body is to take the input pixel, multiply its channels by a percentage between 0 and 100% (determined by control 5), and assign the result to the corresponding output pixel.
 

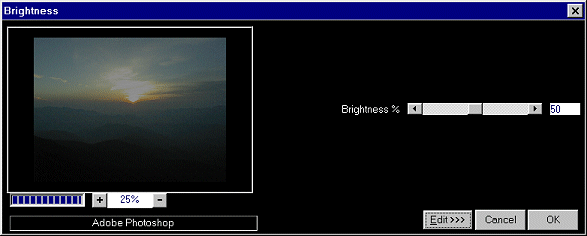
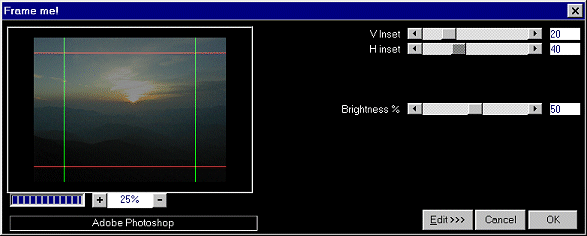
However, the FD is not limited to assigning the output pixel values in any fixed order.  In the following program, we first iterate through all the image pixels in the customary left-to-right, top-to-bottom order, setting the output image to some reduced brightness version of the input image as in the program above.  However, we then use two more for-loops: The first loop iterates from left-to-right across the image, drawing two semi-transparent horizontal red lines; the second for-loop iterates from top-to-bottom, drawing two semi-transparent vertical green lines.  The relative positions of these lines can be controlled by sliders 0 and 1.  This technique can be generalized to implement arbitrary line-drawing, polygon-drawing, circle-drawing, and other 2-D shape-drawing primitives.  Similarly, the technique can be used to implement shape-filling primitives.  A future lesson will introduce FM's built-in set of 2-D drawing functions.
 

%ffp   Title:"Frame me!"   ctl(0):"V Inset",val=10,range=(0,Y/2)   ctl(1):"H inset",val=10,range=(0,X/2)   ctl(5):"Brightness %",val=50,range=(0,100)   ForEveryTile:{       setCtlRange(0,0,Y/2);       setCtlRange(1,0,X/2);       for (x=x_start; x < x_end; x++) {           for (y=y_start; y < y_end; y++) {               for (z= 0; z < Z; z++) {                   pset(x,y,z,src(x,y,z)*ctl(5)/100);               }           }       }       for (x=x_start; x < x_end; x++) {           pset(x,ctl(0),0,255);       //set red channel to max          pset(x,Y-1-ctl(0),0,255);   //set red channel to max      }       for (y=y_start; y < y_end; y++) {           pset(ctl(1),y,1,255);       //set green channel to max          pset(X-1-ctl(1),y,1,255);   //set green channel to max      }       true;  //done!   }

 
Note the following points in the above example:

• In this example, we iterate x from x_start (inclusive) to x_end (exclusive) instead of from 0 to X; and we iterate y from y_start to y_end instead of 0 to Y.  The difference is that [x_start, x_end) is the range of x coordinates in the current tile, whereas [0, X) is the range of x coordinates for the entire image.  Similarly, [y_start, y_end) is the range of y coordinates in the current tile, whereas [0, Y) is the range of coordinates in the entire image. This would seem to be immaterial here, since the entire image in these examples consists of a single tile.  However, the proxy preview may crop the current tile to just the visible portion of the image, depending on the current zoom factor.

• It is possible that pset() will try to set the value of pixels outside the current tile.  This is harmless, because pset() will simply ignore any such request; it is not necessary to check that x and y lie within the tile before calling pset(x,y,...).

 
• The final statement of the ForEveryTile handler sets the return value to true.  This indicates to FM that all processing of the pixels in the tile has been completed, and it is not necessary to invoke any lower-level handlers such as ForEveryRow and ForEveryPixel.

TIP

If you set the return value of the ForEveryTile handler to false, FM will call the ForEveryRow and ForEveryPixel handlers in turn. The default ForEveryPixel handler simply copies the input pixels directly to the output pixels, thus overwriting any changes to the output pixels made by the ForEveryTile handler.  Since this is probably not what you want to do, make sure you set the return value of ForEveryTile to true to avoid invoking the default ForEveryPixel handler!

• A further bit of fanciness in this filter is that we set the ranges of the "V Inset" and "H Inset" controls dynamically.  To prevent the lines from crossing over, we want to limit the upper range of each control to half the height or half the width of the image, respectively.  This is accomplished by specifying range=(0,Y/2) and range=(0,X/2) in the respective ctl keys.  However, Y and X can change dynamically if the user zooms the preview in or out; so we also adjust the range dynamically within the ForEveryTile handler by calling the built-in setCtlRange() function.

 

5. A Newton Fractal Explorer

The following example is adapted from Chapter 7 of Graphics Programming with Java, by Roger T. Stevens.

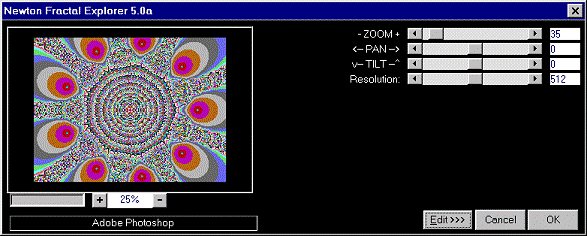
Everyone has seen pictures of the space-filling curves termed "fractals" by Benoit Mandelbrot.  One such class of fractals is based on Newton's method for solving polynomial equations.  Without going deeply into the math involved, we simply present the following program that generates fractal images based on solving a 9-th degree polynomial equation using Newton's method.
 

	TIP
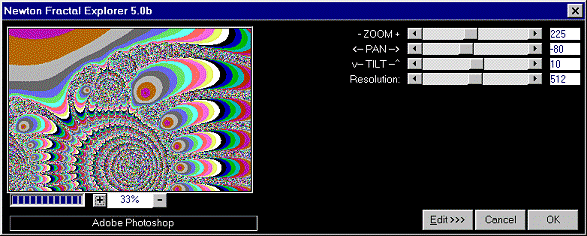
	The filter can take several seconds to update the proxy preview each time a control is adjusted.  For faster "exploring" of the fractal space, zoom the preview out to a scale of 25% or less while panning and tilting; then zoom the preview back in when you spot something interesting!

• The following if-statement is used to test for early convergence to a solution, before the number of iterations specified by the "Resolution" slider is exhausted.  Executing the break-statement causes immediate exit of the immediately surrounding control statement, which in this case is the for-loop controlling the iterations.

• We could have used a switch-statement instead of a cascaded if-statement to set the color of the output pixel.  The switch-statement will be introduced in a future lesson.

	NOT YET IMPLEMEMENTED
	The switch-statement is not yet implemented in release 0.4.4.

• We could have used an array of color values to eliminate the need for the cascaded if-statement altogether.  Arrays will be introduced in a future lesson.

	NOT YET IMPLEMEMENTED
	Arrays are not yet implemented in release 0.4.4.

• The range of the "Resolution" control is 1 to 1024.  The default step size for a scroll bar control is 1 when a scroll bar arrow is clicked (or a cursor key is pressed) or 10 when the scroll bar bed is clicked (or a Page Up/Page Down key is pressed).  These default values are too small for the range 1 to 1024, so we explicitly set the "line" size to 5 and the "page" size to 50 for this control.

• We explicitly update the filter progress indicator by calling the built-in function updateProgress(n,d) to indicate that the filter has completed fraction n/d of the total task.  We call updateProgress() once per row to provide sufficient granularity without the excessive overhead that would be incurred by calling it too often (say, once per pixel). Another trick is that we call updateProgress() once more at the end of the tile to set the progress indication back to zero, thus erasing the progress bar at the end of the filter operation rather than leaving it set at 100%.  Some users find this behavior more satisfactory.

	TIP
	The filter progress indicator is normally updated by the default ForEveryRow handler.  However, setting the return value of the ForEveryTile handler to true causes the ForEveryRow handler to be ignored.  So it is necessary to call updateProgress() explicitly within your ForEveryTile handler to provide the user with visual feedback in this case.

• Finally, note that we call the built-in testAbort() function once per row, and "break" out of the for-loop if the user wants to abort the filter operation.  Normally the default ForEveryRow handler performs this check for us; but again, we are bypassing the invocation of the ForEveryRow handler by returning true from the ForEveryTile handler, so it is necessary to call testAbort() explicitly (at least once per row or so) in order to provide acceptable response to a user's abort request during a long filter operation.

	NOT YET IMPLEMEMENTED
	The testAbort() function tests for a user-requested abort only during final filter application, not during proxy preview processing.  In a future version of FM, testAbort() will also allow the user to abort processing during a proxy preview update.

	TIP
	Since we often want to call testAbort() and updateProgress() at the same place in our filter program, FM provides a shortcut by calling testAbort() implicitly within updateProgress(), and returning the result of testAbort() as the result of updateProgress().  So we can kill two birds with one stone and replace the separate calls to testAbort() and updateProgress() with the following single call:
	// Update the progress indicator and check for   // user abort on each new row...  if (updateProgress(y - y_start, y_end - y_start)) break;

• You can't use pset() to set the value of the current pixel in a ForEveryPixel handler.  Use explicit assignments to R, G, B, or A instead.

• You don't need to call testAbort() and updateProgress() in your ForEveryPixel handler, since the default ForEveryRow handler will do this for you automatically.

• You can't set the progress indicator back to 0 at the end of the filter operation from within the ForEveryPixel handler.  (Well, you can, but it would add unnecessary extra overhead).  You can do this in the OnFinishFilter handler instead; the OnFinishFilter handler will be described in a future lesson.

• In general, there may be a slight speed advantage to using a ForEveryPixel handler instead of coding your own "for every pixel" loop within a ForEveryTile or ForEveryRow handler, since FM uses a highly optimized internal loop to drive the ForEveryPixel handler. However, this speed difference is probably unnoticeable for all but the simplest algorithms.

• The Newton Fractal algorithm presented above has not been optimized for speed, and is designed for didactic purposes only.

Back to the Tutorial Index
 

Home | Download | Documents | Tips & Tutorials | Code Library | Help / User Group | Order