
Home | Download | Documents | Tips & Tutorials | Code Library | Help / User Group | Order

This lesson shows you how to control the order in which your filter processes image pixels by using FM's ForEveryPixel and ForEveryTile handlers in conjunction with for-loops.
This lesson also introduces floating-point arithmetic and the FM built-in functions abs(), src(), pset(), setCtlRange(), updateProgress(), and testAbort().
Throughout this lesson we assume
that the host graphics application is Adobe Photoshop 4.0. The instructions
for other hosts may vary.
| Photoshop 4.0-specific information is flagged with this icon. |
| Information for Paint Shop Pro is flagged with this icon. |
| Features that are not yet implemented are flagged with this icon. |
| Useful tips, techniques, and hints are marked with this icon. |
| This icon indicates a feature that may cause harmful results if improperly used. |
The Filter Designer's sole task is to create a formula for each pixel channel (or plane) that defines the value assigned to each pixel channel as it is processed.
Many image processing algorithms fit naturally into this paradigm, and even more algorithms can be forced to fit (albeit less naturally).
However, there are large classes of algorithms which are difficult to express in this paradigm. FM gives the Filter Designer much greater freedom by allowing the FD to take control of the image processing at the tile, row, or pixel level. At each level, the FD can explicitly control the order of processing by coding his own loops using the various control constructs of the FF+ language.
In this lesson we will concentrate
on controlling the image processing at the tile or pixel level using for-loops.
| %ffp
Title:"Monochrome" R:i |
| %ffp
Title:"Monochrome" ForEveryPixel:
|
At the highest level, FilterMeister processes an image one "tile" at a time, where a tile is a large rectangular section of the input image. The size of each tile is chosen to minimize physical RAM requirements while processing an image. The tile size also depends on the properties of the image processing algorithm. Some algorithms are inherently not tileable; for such "untileable" algorithms, the tile size is set equal to the size of the entire input image, and only one such tile is processed per filter application.
By default, FM takes a conservative approach and considers an algorithm to be untileable. So in the remainder of this lesson, we will assume that each image is processed as a single large tile. The subtleties of writing "tileable" algorithms will be discussed in a future lesson.
The ForEveryTile handler is invoked once for each tile in the input image (which in the following examples means it is invoked once per filter application, with a single tile containing the entire input image).
Within the ForEveryTile
handler, the Filter Designer is free to process the pixels in any desired order
(or even not to process some of them). The FF+ for-loop construct
is useful for controlling the order in which pixels are processed.
for ( <initialization>
; <while-condition> ; <iteration-update> )
{
<body-statements>;
}
where:
In the following program, we use
nested for-loops to iterate through all the pixels of an image, and
all channels within each pixel. The outer for-loop iterates the
x-coordinate (i.e., it iterates left-to-right or column-by-column), the first
inner loop iterates the y-coordinate (from top-to-bottom or row-by-row), and
the innermost loop iterates through the individual channels of each pixel (the
"z" coordinate). Since an inner loop executes many times per iteration of an
outer loop, this means that the y-coordinate varies faster than the x-coordinate.
Thus, we are processing the image column-by-column rather than row-by-row. This
is the transpose of the order in which Filter Factory normally processes an
image.
| %ffp
Title:"Brightness" ctl(5):"Brightness %",val=50,range=(0,100) ForEveryTile:
for
(x=0; x < X; x++) { true;
//Done! |
| TIP | |
| Processing an image in column-by-column order rather than row-by-row order may be useful and important for some algorithms. However, since the image is laid out row-by-row in memory, it is generally more efficient to process row-by-row. Specifically, processing column-by-column may greatly increase the number of page faults for very large images, resulting in slow performance. So if everything else is equal, choose row-by-row rather than column-by-column processing order. |
pset(x, y, z, src(x,y,z)*ctl(5)/100);
The FF/FF+ built-in function src(x,y,z) returns the value of channel
z for the input pixel at coordinates (x,y).
The FF+ built-in function pset(x,y,z,v) sets channel z of the output pixel at coordinates (x,y) to the value v. The value of v is clamped to the range [0,255] before making the assignment.
So the effect of the loop body is
to take the input pixel, multiply its channels by a percentage between 0 and
100% (determined by control 5), and assign the result to the corresponding output
pixel.
However, the FD is not limited to
assigning the output pixel values in any fixed order. In the following
program, we first iterate through all the image pixels in the customary left-to-right,
top-to-bottom order, setting the output image to some reduced brightness version
of the input image as in the program above. However, we then use two more
for-loops: The first loop iterates from left-to-right across the image,
drawing two semi-transparent horizontal red lines; the second for-loop
iterates from top-to-bottom, drawing two semi-transparent vertical green lines.
The relative positions of these lines can be controlled by sliders 0 and 1.
This technique can be generalized to implement arbitrary line-drawing, polygon-drawing,
circle-drawing, and other 2-D shape-drawing primitives. Similarly, the
technique can be used to implement shape-filling primitives. A future
lesson will introduce FM's built-in set of 2-D drawing functions.
| %ffp
Title:"Frame me!" ctl(0):"V Inset",val=10,range=(0,Y/2)
ctl(5):"Brightness %",val=50,range=(0,100) ForEveryTile:{ setCtlRange(0,0,Y/2);
for
(x=x_start; x < x_end; x++) { for
(x=x_start; x < x_end; x++) { for
(y=y_start; y < y_end; y++) { true;
//done! |
| TIP | |
| If you set the return value of the ForEveryTile handler to false, FM will call the ForEveryRow and ForEveryPixel handlers in turn. The default ForEveryPixel handler simply copies the input pixels directly to the output pixels, thus overwriting any changes to the output pixels made by the ForEveryTile handler. Since this is probably not what you want to do, make sure you set the return value of ForEveryTile to true to avoid invoking the default ForEveryPixel handler! |
The following example is adapted from Chapter 7 of Graphics Programming with Java, by Roger T. Stevens.
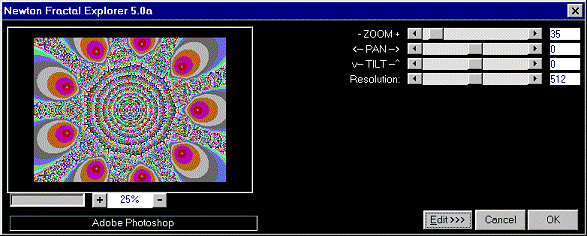
Everyone has seen pictures of the
space-filling curves termed "fractals" by Benoit Mandelbrot. One such
class of fractals is based on Newton's method for solving polynomial equations.
Without going deeply into the math involved, we simply present the following
program that generates fractal images based on solving a 9-th degree polynomial
equation using Newton's method.
| TIP | |
| The filter can take several seconds to update the proxy preview each time a control is adjusted. For faster "exploring" of the fractal space, zoom the preview out to a scale of 25% or less while panning and tilting; then zoom the preview back in when you spot something interesting! |
| %FFP Category: "AFH" Title: "Newton Fractal Explorer 5.0a" Copyright: "Copyright ©1998, AFH Systems Group" Author: "Alex Hunter <alex@afh.com>" Filename: "afhnewton5.8bf" ctl[0]:"- ZOOM +",range=(1,500),val=35
ForEveryTile:
for (y = y_start; y < y_end; y++) {
// Update the progress indicator on each new row...
// Test for user abort request... for (x = x_start; x < x_end; x++) {
x1 = (x - X/2)*100.0/(ctl(0)*X) + ctl(1)/100.0;
for (i0 = 0; i0 < ctl(3); ++i0) { // Reset
progress indicator at end of tile. true;
//completely handled |
| NOT YET IMPLEMEMENTED | |
| The switch-statement is not yet implemented in release 0.4.4. |
| NOT YET IMPLEMEMENTED | |
| Arrays are not yet implemented in release 0.4.4. |
| TIP | |
| The filter progress indicator is normally updated by the default ForEveryRow handler. However, setting the return value of the ForEveryTile handler to true causes the ForEveryRow handler to be ignored. So it is necessary to call updateProgress() explicitly within your ForEveryTile handler to provide the user with visual feedback in this case. |
| NOT YET IMPLEMEMENTED | |
| The testAbort() function tests for a user-requested abort only during final filter application, not during proxy preview processing. In a future version of FM, testAbort() will also allow the user to abort processing during a proxy preview update. |
| TIP | |
| Since we often want to call testAbort() and updateProgress() at the same place in our filter program, FM provides a shortcut by calling testAbort() implicitly within updateProgress(), and returning the result of testAbort() as the result of updateProgress(). So we can kill two birds with one stone and replace the separate calls to testAbort() and updateProgress() with the following single call: | |
|
// Update the progress indicator and check for // user abort on each new row... if (updateProgress(y -
y_start, y_end - y_start)) break; |
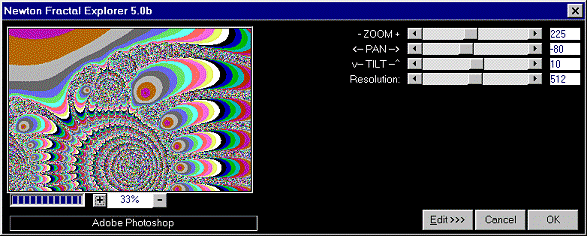
| %FFP Category: "AFH" Title: "Newton Fractal Explorer 5.0b" Copyright: "Copyright ©1998, AFH Systems Group" Author: "Alex Hunter <alex@afh.com>" Filename: "afhnewton5.8bf" ctl[0]:"- ZOOM +",range=(1,500),val=35
ForEveryPixel:
x1 =
(x - X/2)*100.0/(ctl(0)*X) + ctl(1)/100.0; for
(i0 = 0; i0 < ctl(3); ++i0) { } //ForEveryPixel |
Back to the Tutorial
Index
Home | Download | Documents | Tips & Tutorials | Code Library | Help / User Group | Order